トピックス
2020.2.3
スピン流の伝搬機構を偏極中性子で視る
スピン構造物性グループ
今回はスピン構造物性グループの研究を紹介します。
スピン構造物性グループでは、X線や中性子、ミュオンなどの量子ビームと呼ばれる測定手段を用いて、電子スピンが絡む固体物質中の量子現象を対象に研究を展開しています。量子ビームの中でも中性子散乱は非常に強力な微視的測定手段として知られています。中性子は物質中の原子核あるいは不対電子から散乱され、それぞれ結晶格子、磁性の情報を与えてくれます。それらの散乱過程は線形応答理論で記述可能であることから、測定強度の定量的理解も可能となっています。そのため、中性子散乱は幅広い固体物質からソフトマターまで、およそ凝縮系と呼ばれる物質群ほぼすべてに適用可能です。今回は中性子散乱の中でも特に、中性子自身の持つスピン自由度を利用した偏極中性子散乱のスピントロニクスへの適用を紹介します。
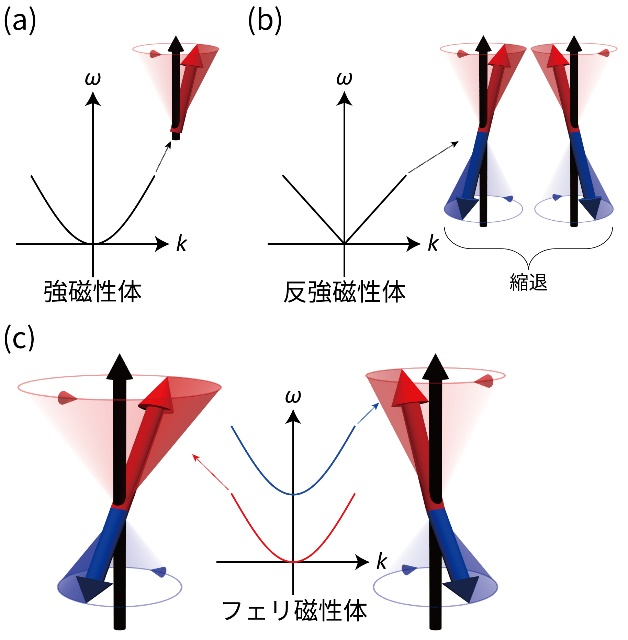
磁性体における磁気秩序の素励起であるスピン波はマグノンと呼ばれる準粒子に量子化されます。このマグノンはボース統計性を持ち、エネルギー、運動量、スピン角運動量を持ちます。磁気モーメントの運動を記述するLandau-Lifshitz-Gilbert(LLG)方程式によると、磁気秩序温度以下では、磁気モーメントは量子化軸の周りを反時計周りに歳差運動します。ここで、この回転方向を正のマグノン極性と定義します。単純な単一ドメインの強磁性体中の磁気モーメントは反時計周りにのみ歳差運動するため、強磁性体は正のマグノン極性を示すと言えます(図1 (a))。共線磁気構造を持つ単純な反強磁性体の場合は、反対の極性を持つ二つのマグノンモードが存在(図1 (b))しますが、巨大な磁場が印加されない限りは通常、これらは縮退しています。つまり、反強磁性体では二つの極性を観察することは難しいことになります。それでは、反強磁性体の二つの副格子のモーメントサイズに差を持たせたフェリ磁性体の場合はどうでしょうか?この場合はモーメントサイズの差を反映してマグノンモードが音響モードとエネルギーギャップを持つ光学モードに分離し、それぞれが反対のマグノン極性を持ちます(図1 (c))。これら二つのモード間のエネルギーギャップは副格子のモーメントサイズの差とスピン間相互作用の積に比例するため、分光学的な測定を用いて検出できる可能性があります。しかしながら、これまで反対の符号を持つマグノン極性について、その直接観測がなされていない状況でした。スピントロニクスにおいて、スピン自由度の流れ、すなわちスピン流は磁気モーメントの歳差運動の横成分によってのみ運ばれます。マグノン極性はこの横成分と数式上共通であるため、スピン流の機構理解のためには、その符号と定量的な測定が必要不可欠です。
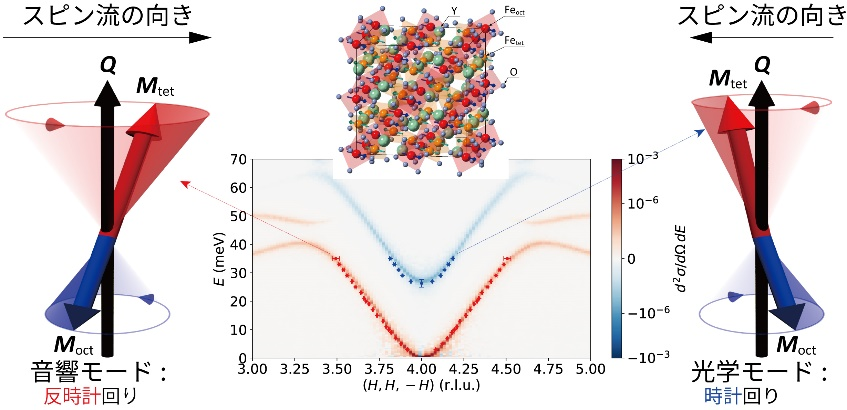
我々は、スピントロニクス研究における代表的な物質Y3Fe5O12(YIG)に着目し、そのマグノン極性検出を行いました [1]。YIGは、複雑な構造を持つフェリ磁性絶縁体(図2)であり、結晶格子の高い対称性を反映して安定した磁化ダイナミクスを示すため、マイクロ波技術や光学技術、あるいはスピントロニクス、マグノニクス、量子情報といった基礎研究に頻繁に利用されています。マグノン極性を観測するには中性子のスピン偏極を散乱ベクトル(Q)方向に向ける必要があります。磁気中性子散乱はQに垂直な面に射影されるスピン成分のみを検出することができます。この場合、Q方向に磁場も印加しているため、Qに垂直な射影成分は非常に微小となり、検出可能な成分は歳差運動が貼る面積のみに対応します。Qに平行な中性子偏極を用いた場合、カイラル項と呼ばれる、Qに垂直な成分のベクトル積に対応する物理量が検出可能であることが知られています。このカイラル項は、時計周りと反時計周りを反対の符号として検出するため、YIGの二つのマグノンモードについてその測定を行いました。図2に得られた実験結果を示します。理論計算と合わせて反対のマグノン極性が明瞭に観測されていることがわかります。図2におけるマグノン歳差運動の絵はQ = 0におけるLLG方程式の解を図示しています。
以上、共線磁気構造を持つフェリ磁性体を用いた初のマグノン極性の観測について紹介しました。この検出されたマグノン極性は、前述のようにスピン流の伝搬方向に直接関係しており、スピントロニクス物質の機構解明には欠かせない微視的情報である点で興味深いものです。今後はこの実験手法を様々な磁性体に適用し、マグノン極性という新しい自由度が絡む物性について開拓していきます。
[1] Y. Nambu et al., Phys. Rev. Lett. 125, 027201 (2020). Editors’ Suggestion